বিস্তার হলো একটি ডেটাসেটের সর্বোচ্চ এবং সর্বনিম্ন মানের মধ্যে পার্থক্য। এটি ডেটাসেটের বিভিন্নতার একটি সহজ পরিমাপ এবং ডেটার বিতরণের প্রাথমিক ধারণা দেয়।
বিস্তার নির্ণয়ের সূত্র:
![]()
উদাহরণ:
ডেটাসেট: 5, 10, 15, 20, 25
বিস্তার: 25 - 5 = 20
বিস্তার পরিমাপ ডেটাসেটের মানগুলোর ছড়িয়ে পড়ার মাত্রা বা ডেটা কতটা ছড়ানো তা বোঝায়। এটি মূলত ডেটাসেটের বৈচিত্র্য এবং স্থিতি নির্ধারণে ব্যবহৃত হয়।
ডেটা বিশ্লেষণে বিস্তার পরিমাপ অত্যন্ত গুরুত্বপূর্ণ, কারণ এটি ডেটার গুণমান এবং স্থিতিশীলতার ধারণা দেয়।
বিস্তার পরিমাপ প্রধানত দুটি ভাগে বিভক্ত:
এটি ডেটাসেটের বাস্তব পরিমাপ ব্যবহার করে বিস্তার নির্ণয় করে। সাধারণত এই ধরনের পরিমাপ ডেটাসেটের বিভিন্নতার সঠিক মান প্রকাশ করে। এর প্রধান প্রকারগুলো হলো:
ক. বিস্তার (Range):
সর্বোচ্চ এবং সর্বনিম্ন মানের মধ্যে পার্থক্য।
Range = Maximum Value -Minimum Value
খ. আন্তঃচতুর্থাংশ বিস্তার (Interquartile Range):
ডেটাসেটের ৭৫তম শতাংশক (Q3) এবং ২৫তম শতাংশক (Q1)-এর মধ্যে পার্থক্য।
IQR = Q3 - Q1
গ. চতুর্ভাগীয় বিচ্যুতি (Quartile Deviation):

ঘ. গড় বিচ্যুতি (Mean Deviation):
ডেটাসেটের প্রতিটি মানের গড় থেকে বিচ্যুতির গড়।
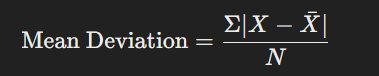
আপেক্ষিক বিস্তার পরিমাপ ডেটার বিভিন্নতার তুলনামূলক মাত্রা নির্দেশ করে এবং এটি সাধারণত শতাংশে প্রকাশিত হয়। এর প্রধান প্রকারগুলো হলো:
ক. আপেক্ষিক গড় বিচ্যুতি (Relative Mean Deviation):
গড় বিচ্যুতিকে গড়ের সাথে তুলনা করে নির্ণয় করা হয়।

খ. আপেক্ষিক চতুর্ভাগীয় বিচ্যুতি (Relative Quartile Deviation):

গ. আপেক্ষিক মান বিচ্যুতি (Relative Standard Deviation):
ডেটাসেটের মান বিচ্যুতিকে গড় বা মধ্যকের সাথে তুলনা করা হয়।

১. ডেটাসেটের বৈচিত্র্য এবং স্থিতি নির্ধারণে সহায়তা করে।
২. বিভিন্ন ডেটাসেটের তুলনা করতে ব্যবহৃত হয়।
৩. গাণিতিক বিশ্লেষণে ডেটাসেটের স্থায়িত্ব যাচাই করা যায়।
৪. ডেটার চরম মান শনাক্তে সহায়তা করে।
বিস্তার এবং বিস্তার পরিমাপ ডেটাসেটের বৈচিত্র্য বোঝার জন্য গুরুত্বপূর্ণ। এটি ডেটার বিস্তৃতি এবং বিভাজন সম্পর্কে একটি পরিষ্কার ধারণা দেয়। বিভিন্ন ধরনের বিস্তার পরিমাপ বিভিন্ন পরিস্থিতিতে ব্যবহৃত হয়, যা ডেটা বিশ্লেষণে অত্যন্ত কার্যকর।